La técnica de Sudoku Y-Wing (Ala-Y) es una técnica bastante avanzada de la resolución de Sudoku que permite eliminar las variantes potenciales en las filas o columnas determinadas en la cuadrícula. Es por ello que este método es conocido como la estrategia de eliminación de candidatos.
De manera similar a la estrategia de Sudoku X-Wing, la del Ala-Y consiste en encontrar un patrón determinado de candidatos en la cuadrícula, pero a diferencia del Ala X afecta solamente tres celdas diferentes, pero no las cuatro. Debido a ello esta estrategia recibe también el nombre de "triples doblados” o el "XY-Wing".
Aunque este patrón no es tan fácil detectar, a veces el semejante enfoque sirve muy bien para resolver las posiciones complicadas de Sudoku.
Ahora bien, ¿qué patrón es este y cómo se puede utilizar la estrategia de Sudoku Y-Wing para resolver rompecabezas?
Patrón Sudoku Y-Wing
El patrón Sudoku Y-Wing se compone de tres celdas diferentes, cada una de las cuales contiene dos de los tres posibles candidatos. Por ejemplo, ab, ac y bc. Es decir, hay tres candidatos posibles con los que estamos trabajando: a, b y c, y dos de estos tres candidatos son los únicos posibles candidatos en las tres celdas. Estas tres celdas también han de formar el patrón Y para que solo una de las tres celdas "vea" (es decir, divida la columna, fila o región 3x3) con las dos otras.
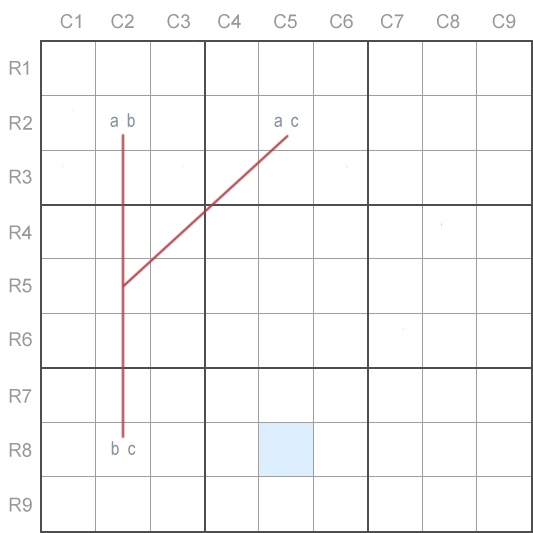
Véase un ejemplo ofrecido a continuación del patrón Sudoku Y-Wing para imaginar claramente qué aspecto esto tiene.

En este ejemplo tenemos tres celdas con los candidatos posibles a, b y c.
Es importante comprender que cada una de estas celdas puede contener solo un candidato correcto. Tampoco podrán contener ninguno de los demás números, salvo los números que están representados como candidatos mostrados anteriormente.
Un par de las líneas rojas había sido añadido para demostrar como este patrón recibió el nombre de "Ala-Y".
Hay que señalar otro momento importante que solamente una de esas casillas "ve" a las dos otras. En este caso es la celda R2C2 ("ab").
¿Qué significa este patrón?
Si pensemos de las consecuencias de este patrón, se hará claro que la celda "ab" puede contener o "a" o "b", entonces "ac" o "bc" deben contener "c". No podrá ser que ni "ac", ni "bc" no contengan "c". Si "ac" contenga "a" y "bc" contenga "b", entonces de acuerdo con las reglas de Sudoku la resolución para la celda "ab" sería imposible.
Haciendo un paso más de conformidad con esta lógica, podemos eliminar el número "c" de cualquier celda que "ve" tanto "ac", como también y "bc", ya que conocemos que una de estas celdas contiene "c". En este ejemplo concreto ello significa que "c" se puede eliminar de la celda R8C5 señalada a continuación.
Utilización de la estrategia Y Wing en la práctica
Ahora, cuando usted conoce que aspecto tiene el patrón Y, vamos a ver como el mismo puede ayudar en la resolución de Sudoku. Para ello vamos a examinar el ejemplo expuesto a continuación.
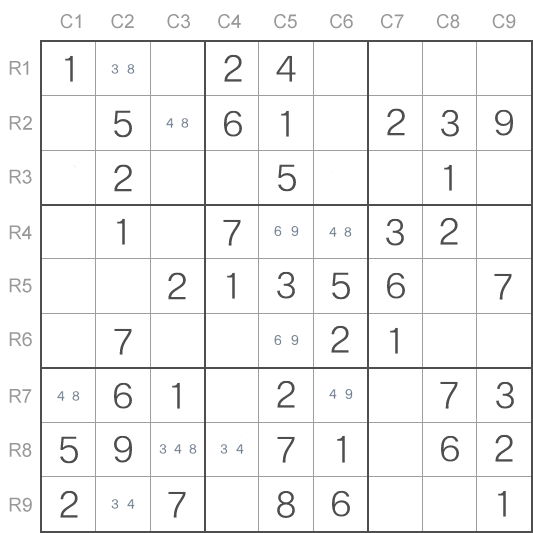
En este ejemplo en algunas celdas se marcan con lápiz todos los candidatos posibles.
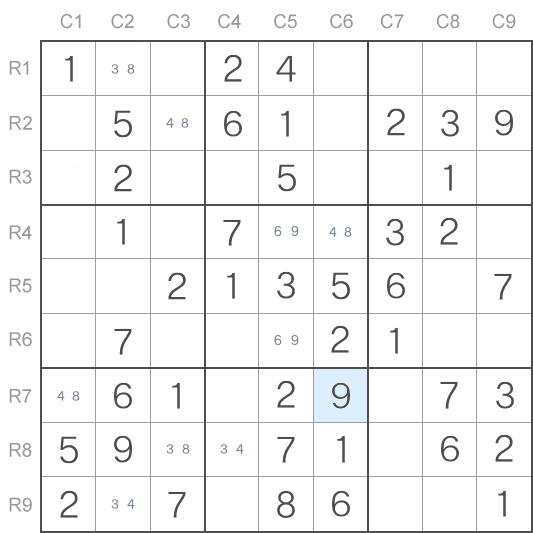
Si mira atentamente, verá que en las columnas C2 y C3 hay un Ala Y de Sudoku con los candidatos 3, 4 y 8. Esto va mostrado a continuación.
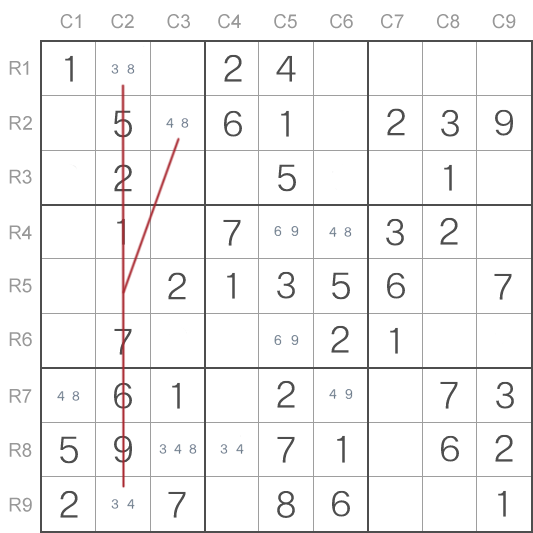
Ahora, cuando hemos identificado el Ala Y, el paso siguiente será la determinación qué de las tres celdas reconoce a las dos demás.
En este caso es la celda superior con los candidatos 3 y 8 (R1C2). Esto significa que una de las dos otras celdas debe contener el número 4. Al hacer un paso más adelante, ahora podemos eliminar el 4 de cualesquier celdas que ven estas dos celdas (R2C3 - "4,8" y R9C2 - "3,4"). Por eso podemos eliminar el 4 como un candidato posible de la celda en la columna C3, fila R8 (marcado en el cuadro situado a continuación.

Ahora, cuando esta celda contiene solo los candidatos 3 y 8, se había formado un Ala Y más. Ahora es horizontal y no vertical, lo que hace más difícil su detección.
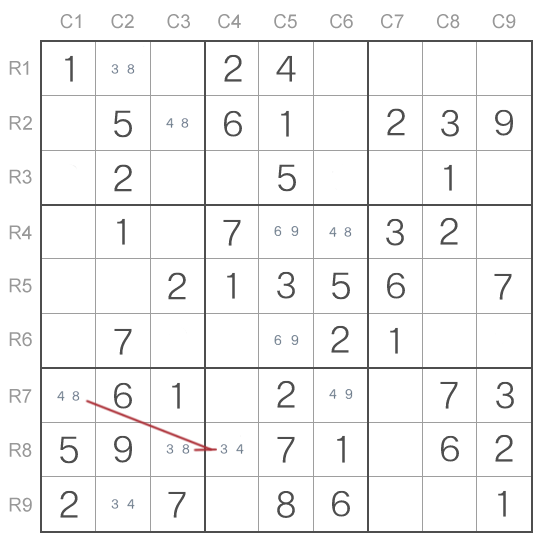
Por eso más útil sería pensar en las Alas Y que en los "triples doblados".
Utilizando el Ala Y recientemente descubierto, podemos ahora eliminar el 4 como candidato de la celda en la columna C6, la fila R7. Ello significa que en la celda se halla el número 9.
Resumen
Como ya había comprendido, la técnica de Sudoku Y-Wing es una técnica avanzada de resolución y no siempre es fácil detectarla.
Por eso no vale usarla para resolver los rompecabezas simples con bajo nivel de complicación. Pero a la medida del aumento de la complicación probablemente tropieza con momentos, cuando es necesario utilizar Y Wing para resolver un rompecabezas. Y ahora, cuando conoce lo que hay que buscar, podrá lograr resolver este Sudoku más complicado.